Analyzing the Most Common Characteristics of Quadratic Functions

Quadratic functions are a type of mathematical equation with two variables, typically represented by the letters x and y. These functions are characterized by the presence of two constants, a, b, and c, and the equation takes the form of ax²+bx+c=0. Quadratic functions can be used to model a wide range of phenomena, from economics to physics.

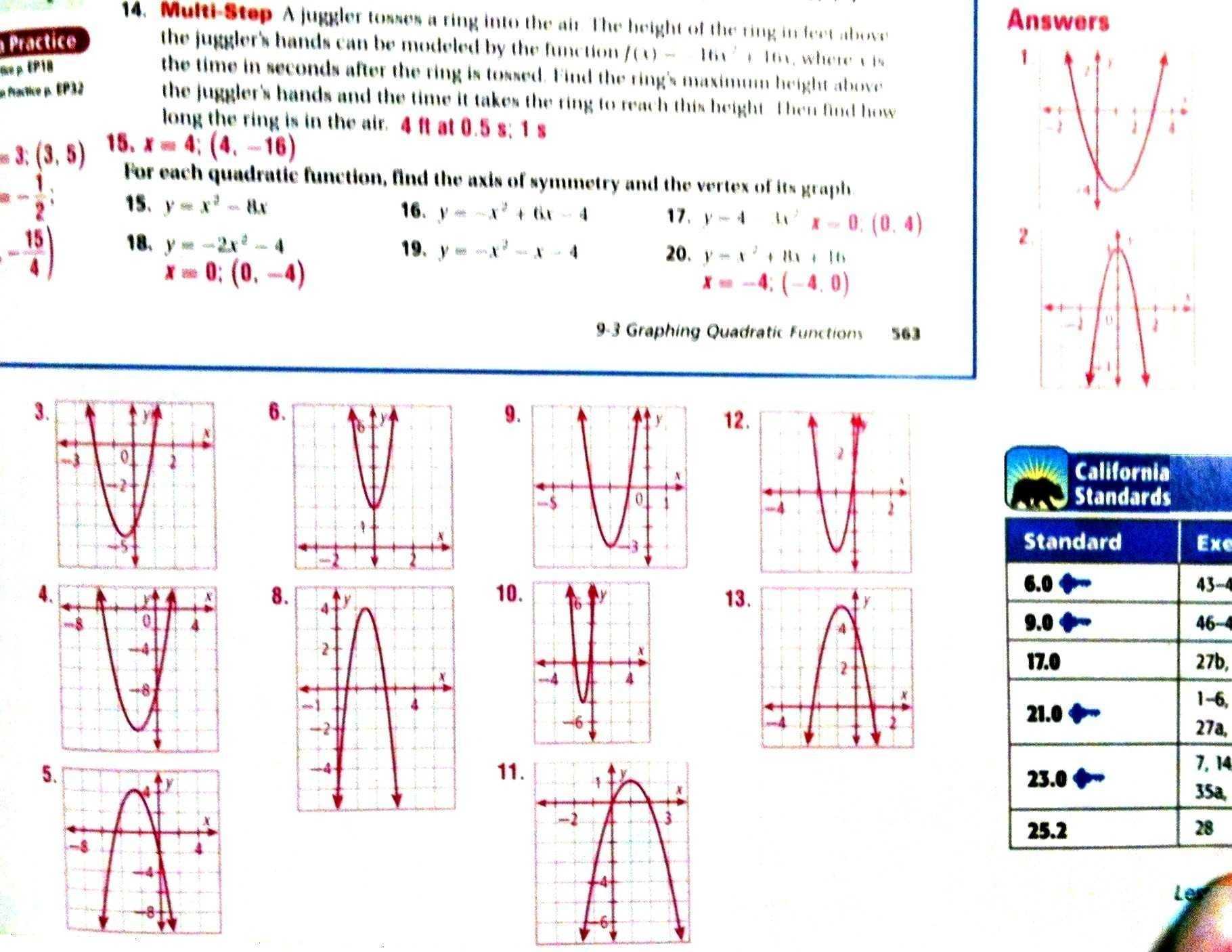
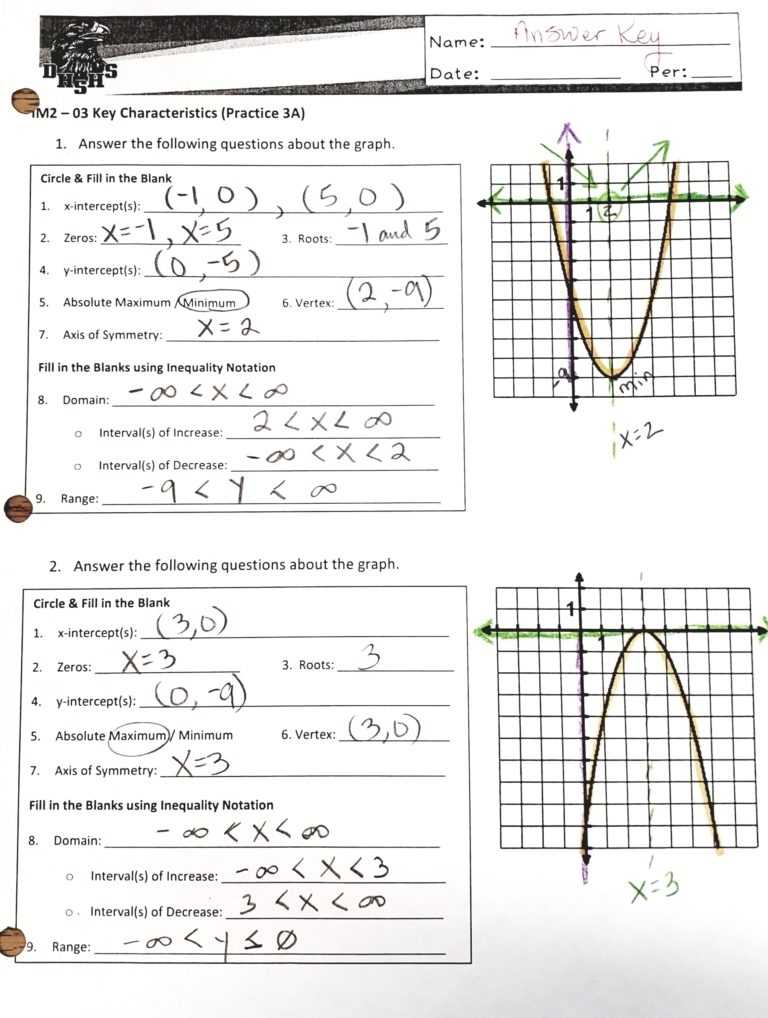
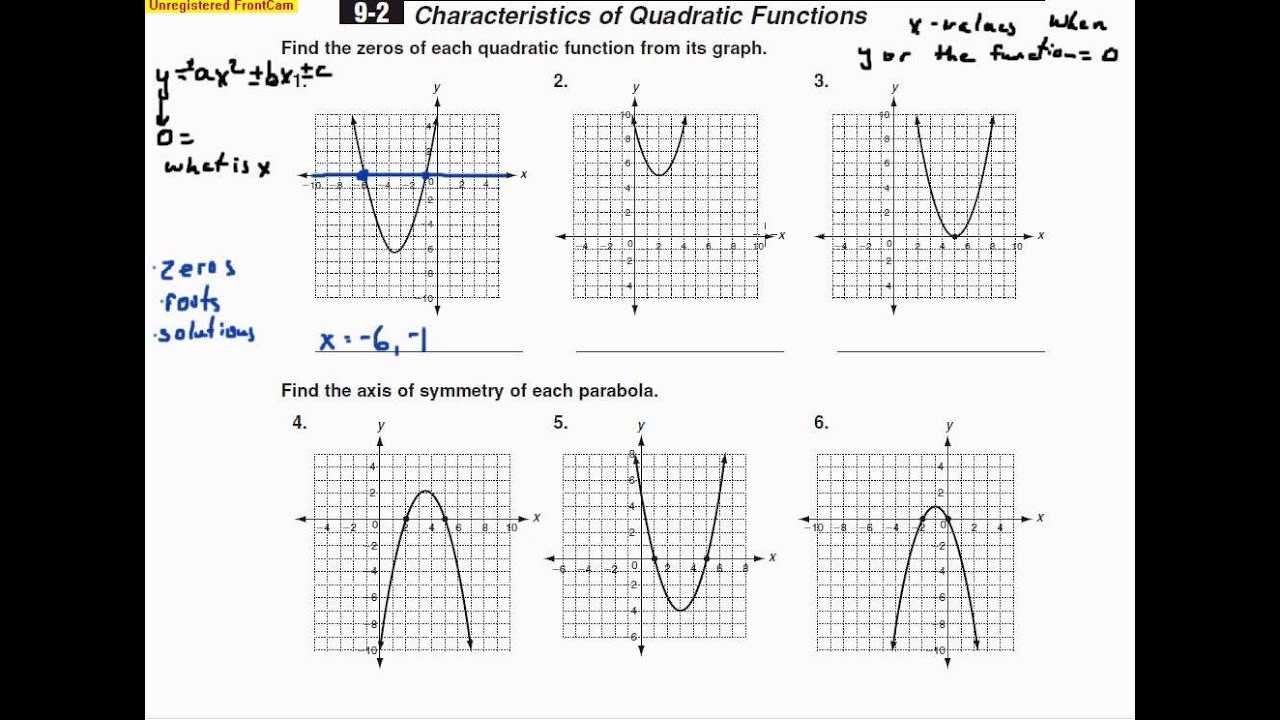
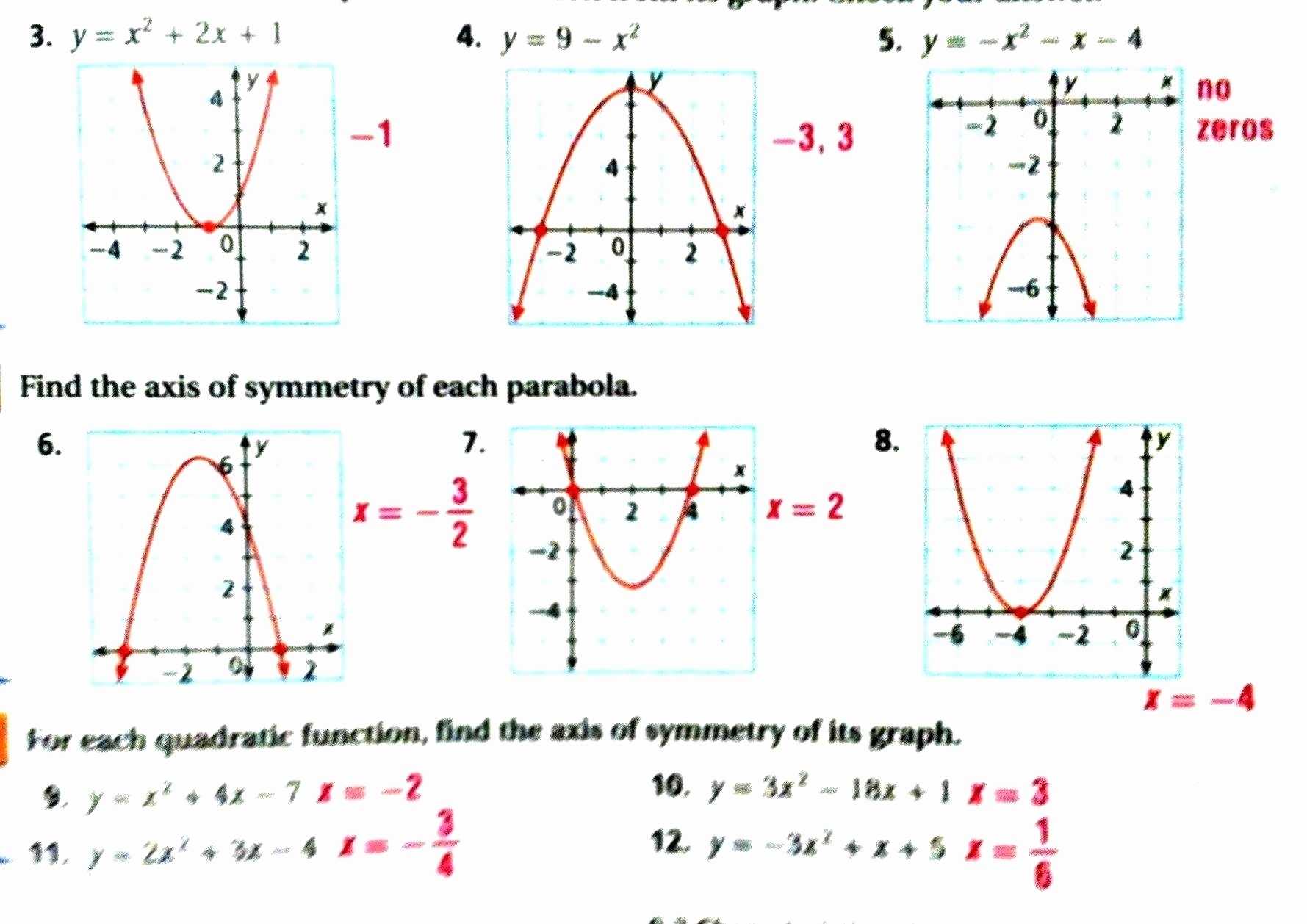
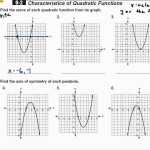
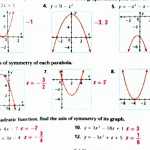
A common characteristic of quadratic functions is that they have a distinct shape, known as a parabola. This shape is produced by the quadratic equation, which is a second-order polynomial equation. The parabola produced by a quadratic equation will always have a vertex and two distinct roots, or solutions. The vertex marks the point on the graph where the parabola reaches its highest or lowest point, depending on its orientation. The roots of the quadratic equation are the two points where the parabola intersects the x-axis.

Another common characteristic of quadratic functions is that they can be expressed in terms of their vertex and roots. By using the vertex form of the equation, which is written as y=a(x-h)²+k, the vertex and roots can be identified. The variable h represents the x-coordinate of the vertex, and the variable k represents the y-coordinate of the vertex. The roots of the equation can then be determined by setting the equation equal to zero and solving for x.

[toc]

Finally, quadratic functions also have a characteristic graph. The graph of a quadratic equation will always be a parabola that opens either up or down. The direction of the graph is determined by the sign of the a-constant. If the a-constant is positive, the parabola will open up, and if the a-constant is negative, the parabola will open down.

In conclusion, quadratic functions are characterized by their distinct shape, their ability to be expressed in terms of their vertex and roots, and their characteristic graph. These characteristics make quadratic equations a powerful tool for modeling a wide range of phenomena.

Exploring How to Use a Quadratic Functions Worksheet to Solve Problems

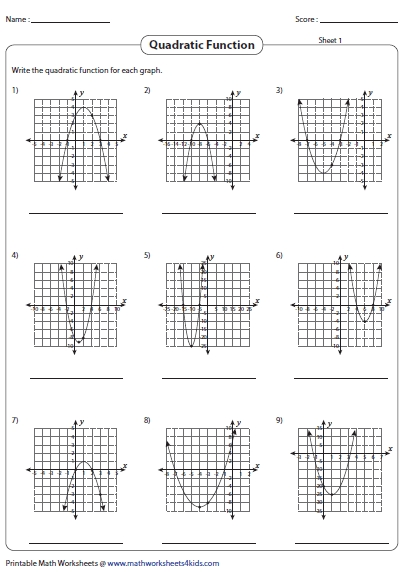
A quadratic functions worksheet can be a powerful tool for solving a variety of mathematical problems. This type of worksheet consists of a set of equations that represent quadratic functions, which are equations of the form y = ax^2 + bx + c. By using the worksheet, students can gain an understanding of how to use the quadratic equation and its properties to solve a variety of problems.

The first step in using the quadratic functions worksheet is to identify the equation of the quadratic function. Once the equation has been identified, the student can then use the quadratic formula to solve for the unknown variables. The quadratic formula is a mathematical formula that allows the student to isolate a specific term in the equation and then solve for that term. This allows the student to determine the values of the unknown variables in the equation.

Once the student has determined the values of the unknown variables, they can then use the information to solve the problem. To do this, the student must first identify the solutions of the equation and then use the solutions to solve the problem. Depending on the complexity of the problem, the student may have to use multiple solutions to solve the problem.

Once the student has solved the problem and has identified the solutions, they can then use the quadratic functions worksheet to graph the solutions. By graphing the solutions, the student can identify the x-intercepts, y-intercepts, and the slopes of the equation. This allows the student to visualize how the solutions of the equation relate to one another and to the equation itself.

By using the quadratic functions worksheet to solve a variety of problems, students can gain an understanding of how to use quadratic equations and its properties to solve problems. In addition, students can gain a better understanding of the properties of quadratic equations and how to use them to solve a variety of problems. With this knowledge, students can use the quadratic functions worksheet to become more proficient in solving a variety of mathematical problems.

Understanding Quadratic Functions: A Comprehensive Guide to Working with Quadratic Equations

Quadratic functions represent an important branch of mathematics and are essential to understand when working with equations. In this guide, we will cover the fundamentals of quadratic functions and how to work with them.

A quadratic function is a polynomial of degree two. It is written as an equation of the form ax2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. This equation can also be written in the form y = ax2 + bx + c, which gives the graph of the quadratic function.

The graph of a quadratic function is a parabola. It has a single vertex and two distinct roots. The vertex is the point at which the graph changes direction and is located at the point (x, y) = (−b/2a, f(-b/2a)). The roots of the equation are the x-intercepts of the graph, which are found by setting the equation equal to zero and solving for x.

To solve quadratic equations, the quadratic formula can be used. The formula is x = (-b ± √b2 – 4ac) / 2a. This formula can be used to find the roots of any quadratic equation.

Factoring is another important method for solving quadratic equations. This method involves factoring the equation into the form (ax + b)(cx + d) = 0 and then solving for x. This method can be used when the coefficient of the x2 term is one.

It is also important to understand the concept of completing the square. This method involves rewriting the equation in the form (x + b/2a)2 + c – b2/4a = 0 and then solving for x.

In addition to solving quadratic equations, it is also useful to understand how to use quadratic functions to model real-world situations. Quadratic functions can be used to model the height of a projectile, the cost of production, or the demand for a product, among other applications.

Finally, quadratic equations can be used to solve more complex problems. By understanding the basics of how to work with quadratic equations, it is possible to solve problems such as finding the maximum or minimum of a function, finding points of intersection, finding the equation of a tangent line, and much more.

This comprehensive guide provides the fundamentals of quadratic functions and how to work with them. With this knowledge, it is possible to solve a variety of equations and model real-world situations.

Conclusion

The Characteristics Of Quadratic Functions Worksheet is a great resource for students to gain a better understanding of the topic. It provides detailed explanations of the different characteristics of quadratic functions, as well as a variety of practice problems which allow students to apply their knowledge. With this worksheet, students can gain a better insight into the relationship between the graph of a quadratic function, its roots, and the equation of the function. This knowledge can be used to solve a variety of real-world problems.

[addtoany]