A Comprehensive Guide to Finding the Measurements of Central and Inscribed Angles in a Circle
A circle is a two-dimensional shape with a single curved line as its perimeter and a single point at its center. Its unique shape makes it an interesting and often studied figure in mathematics. One of the most common questions about circles is how to find the measurements of the angles that can be formed within them. This guide will explain how to find the measurements of the central and inscribed angles in a circle.
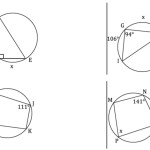
Central angles are angles that are formed by two radii (lines from the center of the circle to its perimeter) of a circle. The measurement of a central angle is determined by the fraction of the circumference of the circle that it encompasses. To find the measurement of a central angle, divide the circumference of the circle by the number of degrees in the angle. For example, if the circumference of the circle is 360 units and the angle is 120 degrees, the measurement of the central angle would be (360/120) 3 units.
Inscribed angles are angles that are formed by two chords (lines connecting two points on the perimeter of a circle) in a circle. The measurement of an inscribed angle is determined by the fraction of the central angle that the inscribed angle is subtending. To find the measurement of an inscribed angle, multiply the total number of degrees in the central angle by the fraction of the central angle that the inscribed angle is subtending. For example, if the central angle is 120 degrees and the inscribed angle is subtending one-third of the central angle, the measurement of the inscribed angle would be (120 x 1/3) 40 degrees.
[toc]
By using these formulas, you can easily calculate the measurements of both central and inscribed angles in a circle. Knowing how to calculate these measurements can be useful for a variety of mathematical problems, such as calculating the area of a segment of a circle.
Exploring the Relationship Between Central and Inscribed Angles in a Circle
The relationship between central and inscribed angles in a circle is a fascinating topic of study. Central angles are those that have their vertex at the center of the circle, while inscribed angles are those that have their vertex at a point along the circumference. Both types of angles have unique characteristics that can be explored to gain a better understanding of their relationship.
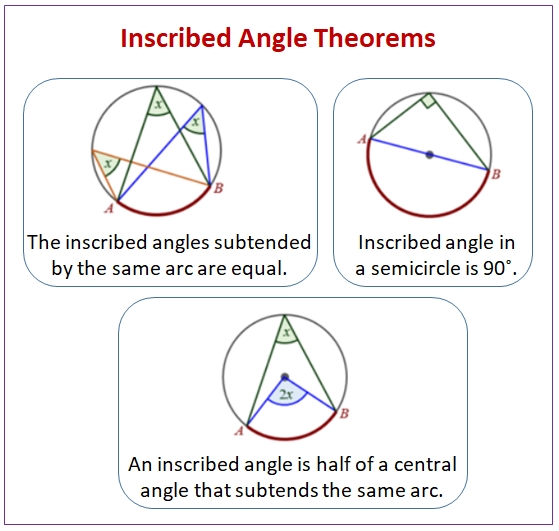
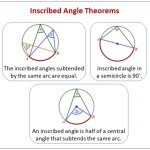
In regards to central angles, they are always equal in measure to the intercepted arc that they contain. Thus, the measure of the angle is directly proportional to the arc length. This property can be used to find the measure of a central angle when its arc is known, or vice versa.
Inscribed angles, on the other hand, have a measure that is half the measure of the intercepted arc. As with central angles, this property can be used to find the measure of the angle if the arc length is known.
Furthermore, an interesting relationship exists between central and inscribed angles. If a central angle and its corresponding inscribed angle are drawn, they will always be supplementary angles, meaning that the sum of their measures will equal 180°. This property can be used to find the measure of either angle when the measure of the other is known.
Ultimately, the relationship between central and inscribed angles is one of great complexity and interest. Through further study, even more properties can be uncovered.
How to Use a Central and Inscribed Angle Worksheet to Help Improve Student Understanding
Using a central and inscribed angle worksheet can be an effective way to help students become more comfortable and proficient in understanding the concepts of central and inscribed angles. Teaching these concepts can be a challenging task, as students often struggle with the relationship between central and inscribed angles, as well as how to measure them. A central and inscribed angle worksheet can help to improve student understanding by providing a visual tool for them to use.
The worksheet typically consists of several circles with a number of angles labeled on each. The angles are then labeled as either central or inscribed angles. This allows students to visually see the relationship between the two angles, as well as the angles that are formed by the intersection of two lines. This can help to clarify the differences between the two angles and better illustrate how to measure them.
The worksheet also includes examples of measurements for the different angles. This gives students an opportunity to practice measuring angles and helps to reinforce the concept of measuring angles with a ruler or protractor. The worksheet can also include questions that ask students to apply the concepts to the angles on the worksheet. This can help to further reinforce the understanding of central and inscribed angles.
By providing students with a visual tool to work with and practice with, a central and inscribed angle worksheet can help to improve student understanding of the concepts. This can be a useful tool for any teacher who is looking to help their students get a better grasp of the concepts of central and inscribed angles.
A Step-by-Step Guide to Solving Central and Inscribed Angle Problems with Worksheets
Central and inscribed angles are important concepts in geometry and trigonometry. They are useful in solving a variety of geometric problems, such as determining the length of a line segment or the area of a triangle. Knowing how to solve central and inscribed angle problems can be a valuable skill to have in mathematics. This guide will provide step-by-step instructions and worksheets to help you learn how to solve central and inscribed angle problems.
Step 1: Understand the Terms
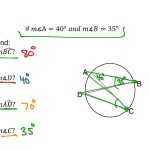
Before attempting to solve any central or inscribed angle problems, it is important to understand the definitions of the terms. A central angle is an angle whose vertex is located at the center of a circle. An inscribed angle is an angle whose vertex lies on the circumference of a circle.
Step 2: Understand the Problem
The next step is to understand the problem. Read the problem carefully and make sure you understand what it is asking. Pay attention to any given information, such as the size of the angle or the measure of the radius.
Step 3: Determine the Measure of the Angle
The next step is to determine the measure of the angle. If the problem provides the measure of the angle, then you can skip this step. If the measure of the angle is not given, then you must use the formula for the measure of a central or inscribed angle to calculate it.
For central angles, the formula is:
M = (n – 2) * 180 / n
For inscribed angles, the formula is:
M = 180 / n
Where n is the number of points or sides of the polygon that the angle intersects.
Step 4: Calculate the Length of the Line Segment
Once you have determined the measure of the angle, you can use the Law of Cosines to calculate the length of the line segment.
For central angles, the formula is:
a^2 = b^2 + c^2 – 2bc * cos(A)
For inscribed angles, the formula is:
a^2 = b^2 + c^2 – 2bc * cos(B / 2)
Where a is the length of the line segment, b and c are the lengths of the two radii that make up the angle, and A and B are the measures of the central and inscribed angles, respectively.
Step 5: Calculate the Area of the Triangle
Once you have calculated the length of the line segment, you can use Heron’s formula to calculate the area of the triangle. Here is the formula:
A = √(s * (s – a) * (s – b) * (s – c))
Where s is the semiperimeter of the triangle, a, b, and c are the lengths of the sides of the triangle, and A is the area of the triangle.
Step 6: Check Your Work
Once you have calculated the measure of the angle and the length of the line segment, you should check your work. Make sure your answers make sense in the context of the problem.
Worksheets
The following worksheets can be used to practice solving central and inscribed angle problems.
Worksheet 1:
1
An Overview of the Different Types of Central and Inscribed Angle Worksheets Available
Central and inscribed angle worksheets are a great way to practice the essential mathematical concepts of angle size and shape. They can be used by students from elementary school through college level to help them understand the basics of angle measurement and geometry. There are a variety of worksheets available, each with its own distinct purpose.
The first type of worksheet is the basic central and inscribed angle worksheet. This worksheet provides students with the opportunity to practice finding the measure of angles formed by intersecting lines. It can also be used to practice finding the measures of angles formed by lines that cross at one point, as well as angles formed by intersecting circles.
The second type of worksheet is the inscribed angle worksheet. This worksheet focuses on the study of angles formed by intersecting circles. It can be used to practice finding the measure of angles formed by two circles intersecting at one point or two circles intersecting at multiple points.
The third type of worksheet is the central angle worksheet. This worksheet focuses on finding the measure of an angle formed by a circle and a line. It can be used to practice finding the measure of angles formed by a circle and a line, as well as angles formed by multiple circles and multiple lines.
Finally, the fourth type of worksheet is the arc length and sector area worksheet. This worksheet focuses on finding the length of a circle’s arc, as well as the area of a circular sector. It can be used to practice finding the length of an arc or the area of a sector.
These four types of worksheets can provide students with the practice they need to properly and accurately measure angles and circles. They can help students understand the fundamentals of geometry, as well as help them prepare for more advanced math courses.
Analyzing the Effects of Changing Radius and Chord Lengths on Central and Inscribed Angles
The central angle and inscribed angle of a circle are two important concepts in geometry and often appear in geometric problems. The central angle of a circle is an angle constructed from two radii, while an inscribed angle is an angle constructed from two chords. It is important to understand the relationships between the radius, chord lengths, and the central and inscribed angles. This article will discuss the effects of changing the radius and chord lengths on the central and inscribed angles.
The central angle is an angle formed by two radii that start from the center of the circle and meet at a point on the circumference of the circle. The central angle is equal to the ratio of the arc length formed by the radii and the circumference of the circle. As the radius of the circle increases, the central angle also increases. If the radius of the circle is reduced, the central angle will be reduced as well.
The inscribed angle is an angle formed by two chords that start from one point on the circumference of the circle and meet at another point. The inscribed angle is equal to half the central angle formed by the two intersecting chords. When the length of the chord is increased, the inscribed angle also increases. Conversely, when the chord length is reduced, the inscribed angle will also be reduced.
In summary, the radius and chord lengths of a circle have an effect on the central and inscribed angles formed. As the radius of the circle increases, the central angle also increases, while when the radius is reduced, the central angle decreases. Similarly, as the length of the chord increases, the inscribed angle also increases, while when the chord length is reduced, the inscribed angle decreases.
Exploring the Benefits of Using Central and Inscribed Angle Worksheets in the Classroom
Central and inscribed angle worksheets are a powerful tool for introducing geometry concepts to students in the classroom. By using these worksheets, teachers are able to provide students with hands-on practice in identifying and understanding the relationships between angles, circles, and triangles. In addition, these worksheets can easily be adapted to different levels of difficulty, making them ideal for a wide range of students.
Central and inscribed angle worksheets enable students to develop their knowledge of basic geometric principles through engaging and interactive activities. By completing the activities on these worksheets, students are able to identify and calculate the measurements of central and inscribed angles, as well as identify and understand the relationships between the angles and circles. This helps them to build their geometric reasoning skills and develop their understanding of basic geometry.
In addition to helping students to understand basic geometric principles, central and inscribed angle worksheets can also help to reinforce important concepts. By completing the activities on these worksheets, students are able to visualize how the various angles and circles interact with each other and apply what they have learned to other topics in geometry. This helps to ensure that students are able to transfer their knowledge to other areas of math and science.
Central and inscribed angle worksheets can also be used to introduce new topics in geometry, such as the properties of circles, triangle congruence, and the Pythagorean theorem. By completing the activities on these worksheets, students are able to gain an understanding of the topics that will be covered in class. This helps to ensure that students are well-prepared for the topics that will be discussed in class.
Finally, central and inscribed angle worksheets are also beneficial for teachers. By providing students with hands-on practice in identifying and understanding the relationships between angles, circles, and triangles, teachers are able to better assess student progress and adjust their lesson plans accordingly. This allows teachers to ensure that all students are on the same page and understand the material that is being taught.
In conclusion, central and inscribed angle worksheets are an invaluable asset for teachers in the classroom. By providing students with hands-on practice in understanding the relationships between angles, circles, and triangles, these worksheets enable students to develop their knowledge of basic geometric principles and reinforce important concepts. Additionally, these worksheets can be adapted to different levels of difficulty, making them ideal for a wide range of students. Therefore, it is clear that the benefits of using central and inscribed angle worksheets in the classroom are numerous.
Tips and Tricks for Mastering Central and Inscribed Angle Worksheets
1. Become familiar with the definitions of central and inscribed angles. A central angle is an angle formed by two radii that share a common endpoint at the center of a circle. An inscribed angle is an angle formed by two chords that have the same endpoint on a circle.
2. Familiarize yourself with the theorems related to central and inscribed angles. These theorems can be used to answer questions related to these angles, such as the measure of the central angle if the inscribed angle is known, or vice versa.
3. Review the formulas related to central and inscribed angles. You should be able to recall the formula for the measure of an inscribed angle if the measure of the intercepted arc is known, as well as the formula for the measure of the intercepted arc if the measure of the inscribed angle is known.
4. Memorize the relationship between inscribed angles and arcs. This is an important relationship to know when solving problems related to central and inscribed angles. Remember that the measure of an inscribed angle is equal to half the measure of the intercepted arc.
5. Practice with worksheets and online quizzes. The best way to become comfortable with central and inscribed angles is to practice with a variety of examples. Use worksheets and online quizzes to give yourself more practice opportunities.
6. Draw diagrams to help with understanding. Drawing diagrams can help to visualize the relationships between central and inscribed angles, as well as the relationships between arcs and inscribed angles. This can be especially helpful when solving problems related to these angles.
7. Work with a partner or study group. Working with a partner or study group can be a great way to become more comfortable with central and inscribed angle worksheets. This can allow you to work through problems together and get feedback from each other.
Conclusion
The Central and Inscribed Angle Worksheet is a great resource for students of all levels, from elementary to college, to learn about and practice the concepts of central and inscribed angles. With the worksheet, students can practice identifying the different types of angles, as well as understanding how to calculate the measure of each angle type. This can be a great way for students to increase their confidence in their math skills and understand how to use angles in more complex problems.
[addtoany]