Exploring Arithmetic Sequences and Series: A Comprehensive Worksheet Guide

Introduction

This worksheet guide aims to provide a comprehensive overview of arithmetic sequences and series. Arithmetic sequences and series are mathematical concepts that are fundamental to understanding calculus and higher mathematics. They are composed of numbers that increase or decrease by a constant amount, known as the common difference (or ‘d’). This guide will provide the reader with an understanding of the basics of arithmetic sequences and series, their applications, and how to solve specific problems.

What is an Arithmetic Sequence?

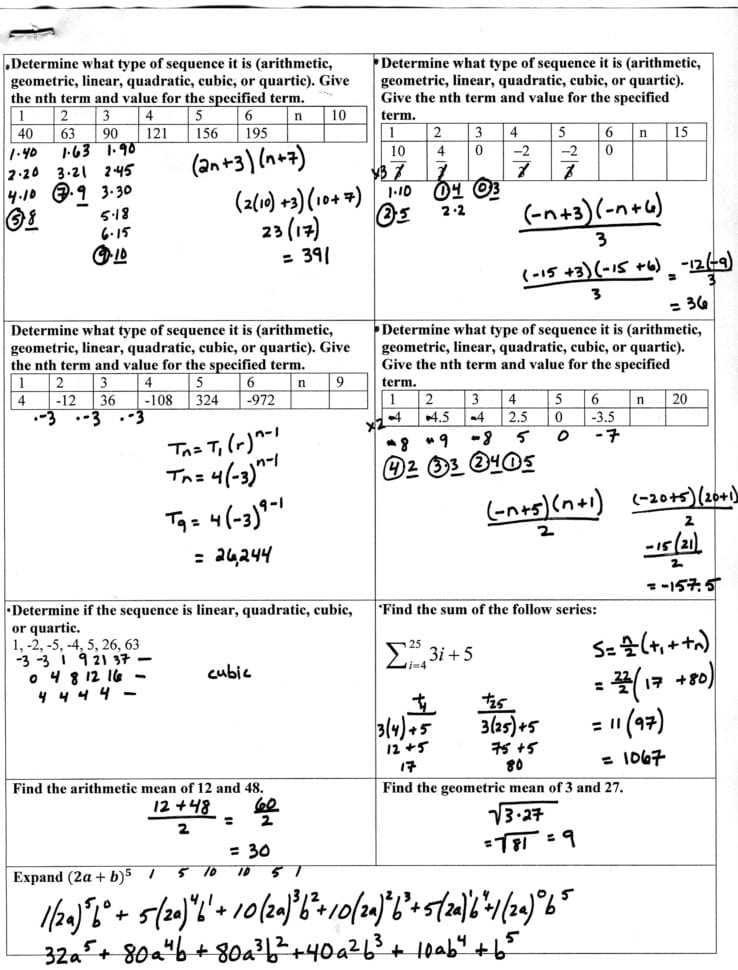
An arithmetic sequence is a sequence of numbers in which each number is obtained by adding a fixed number, the common difference (‘d’), to the previous number. The sequence is composed of numbers that form an arithmetic progression. The first term of the sequence is denoted as ‘a’, and the common difference as ‘d’.

For example, let ‘a’ = 4 and ‘d’ = 3.

The arithmetic sequence would then be 4, 7, 10, 13, 16, 19, 22, etc.

What is an Arithmetic Series?

An arithmetic series is the sum of the terms in an arithmetic sequence. It is calculated by adding the first term to the last term, and then multiplying the result by the number of terms, divided by two.

For example, if the first term of the sequence is 4 and the last term is 22, the arithmetic series would be

(4 + 22) x (10/2) = 132.

How to Solve Problems

In order to solve problems involving arithmetic sequences and series, the following steps should be taken:

1. Identify the first term (‘a’) and the common difference (‘d’).

2. Identify the number of terms in the sequence or series (‘n’).

3. Calculate the last term (‘l’) by using the formula l = a + (n-1)d

4. Calculate the sum of the series using the formula: S = (a + l) x (n/2).

Conclusion

This guide has provided a comprehensive overview of arithmetic sequences and series. It has discussed the basics of the concepts, their applications, and how to solve problems. Understanding arithmetic sequences and series is essential for further study of mathematics, and this guide should provide a solid foundation for students wishing to explore this topic.

Unpacking the Math Behind Arithmetic Sequences and Series Worksheets

Arithmetic sequences and series are a fundamental concept in mathematics that often appears on worksheets. This article will provide an overview of the math behind such worksheets and explain how to use them effectively.

An arithmetic sequence is a sequence of numbers in which each successive number is obtained by adding a constant amount, known as the common difference, to the previous number. The sequence can be written as a mathematical equation in the form of an = a1 + (n-1)d, where a1 is the first term of the sequence, n is the number of terms in the sequence, and d is the common difference.

A series is the sum of the terms of an arithmetic sequence. Series can be written as a mathematical equation in the form of Sn = n/2(2a1 + (n-1)d), where n is the number of terms in the series and a1 and d are the same as before.

Arithmetic sequences and series worksheets generally contain problems in which students must calculate the nth term of a sequence, the sum of the first n terms of a series, or both. In order to solve these problems, students must be familiar with the concepts of arithmetic sequences and series and know how to use the above equations.

In addition to practice problems, worksheets may also include questions that require students to identify the common difference, the first term, or the number of terms in a given sequence or series.

By understanding the math behind arithmetic sequences and series worksheets, students will be better equipped to accurately solve these types of problems.

Utilizing Real-World Examples to Enhance Arithmetic Sequences and Series Worksheets

Arithmetic sequences and series are important mathematical concepts that can be difficult for students to comprehend. To help foster a better understanding of these concepts, real-world examples can be used to enhance the learning experience.

When teaching arithmetic sequences and series, real-world examples can be used to demonstrate how they are used in everyday life. For example, a student can examine the pattern of a bank account balance, which follows an arithmetic sequence. By breaking down the individual components of the sequence, such as the common difference, the student can better understand the concept. Other real-world examples include the pattern of a payroll check, a grocery shopping budget, and the price of a stock over time.

Incorporating real-world examples into worksheets can help students understand the concepts more easily. For example, a worksheet could include a chart or graph of a bank account balance and ask students to identify the pattern of the sequence. The worksheet could also include questions that ask students to calculate the common difference of the sequence or find the sum of the series.

Real-world examples can also be used to help students develop problem-solving skills. A worksheet could include a situation involving a bank account balance or a grocery budget and ask students to use their knowledge of arithmetic sequences and series to determine the best course of action. This type of problem-solving activity can help students apply their knowledge in a practical setting.

In summary, real-world examples can be used to enhance worksheets that focus on arithmetic sequences and series. Incorporating real-world examples into worksheets can help students better understand the concepts and develop their problem-solving skills. By utilizing real-world examples, teachers can foster a deeper understanding of the mathematical concepts and help students apply their knowledge in everyday life.

Conclusion

The Arithmetic Sequences And Series Worksheet is a useful resource for students to practice and gain a better understanding of arithmetic sequences and series. It helps students to identify the characteristics of each type of sequence and series, practice solving related problems, and develop a better understanding of the topics. With this worksheet, students can further their knowledge of arithmetic sequences and series and be better prepared for future math courses.