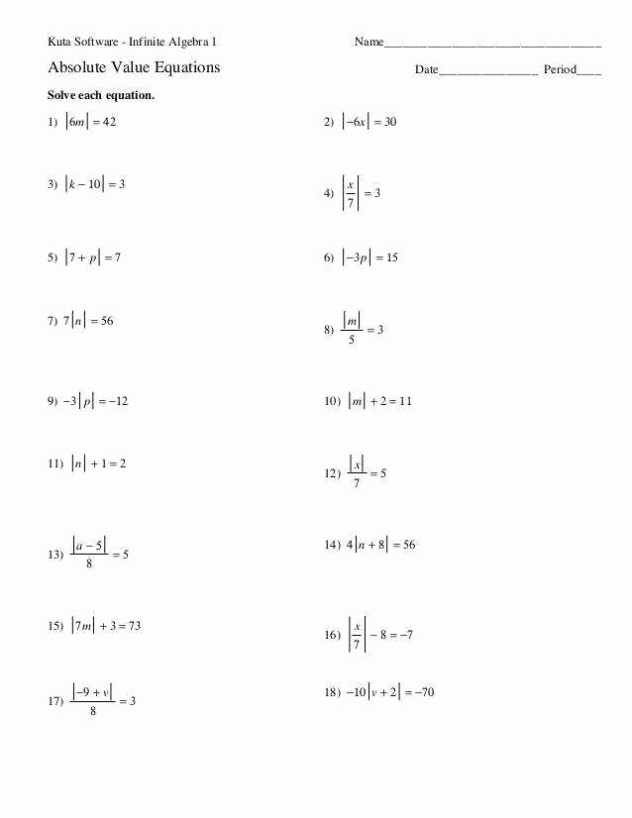Analyzing Absolute Value Inequalities Worksheet Answers: A Guide to Understanding the Basics

The purpose of this guide is to help students understand the basics of analyzing absolute value inequalities. Absolute value inequalities are equations in which the unknown variables are related to one another by an absolute value function. The goal of solving these equations is to determine the range of values for the unknown variables that make the equation true.

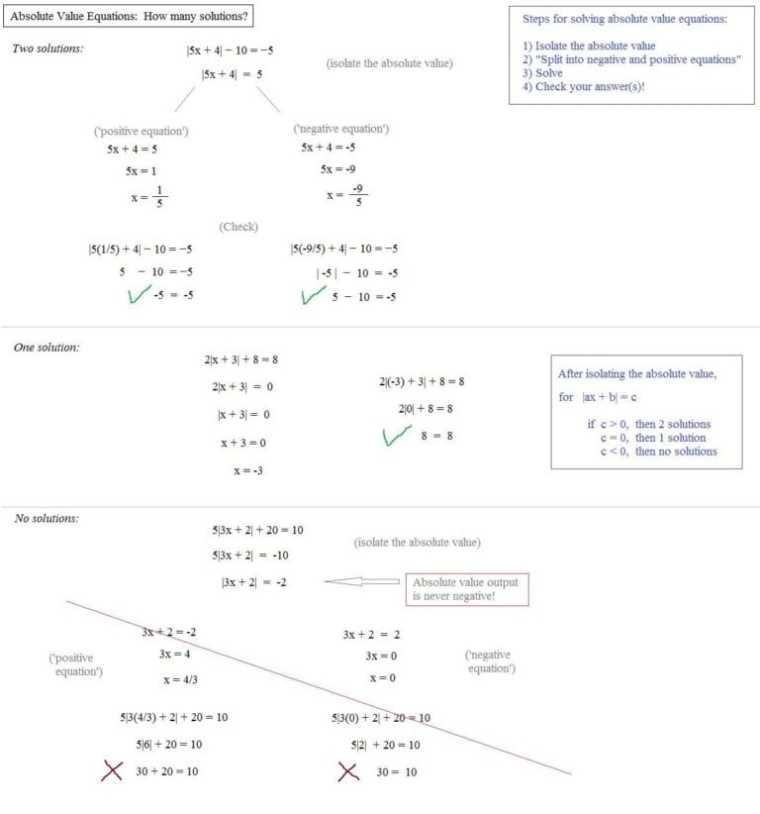
The first step in analyzing absolute value inequalities is to isolate the absolute value term on one side of the equation. This is done by subtracting all terms in the equation from both sides until the absolute value term is the only term on one side of the equation. Once this is done, the equation can be split into two equations, one with the positive absolute value term and one with the negative absolute value term.

Next, the equations are solved by treating the absolute value term as an unknown variable. Each equation is then solved for the unknown variable, resulting in two separate solutions. Finally, the two solutions are combined to form a single solution that satisfies both equations.

[toc]

It is important to note that, when solving absolute value inequalities, all solutions are valid as long as they satisfy the original equation. Therefore, students should carefully check their solutions to make sure that they meet the requirements of the original equation.

By following these steps, students can easily understand the basics of solving absolute value inequalities. With practice and patience, they will quickly become proficient in this type of problem solving.

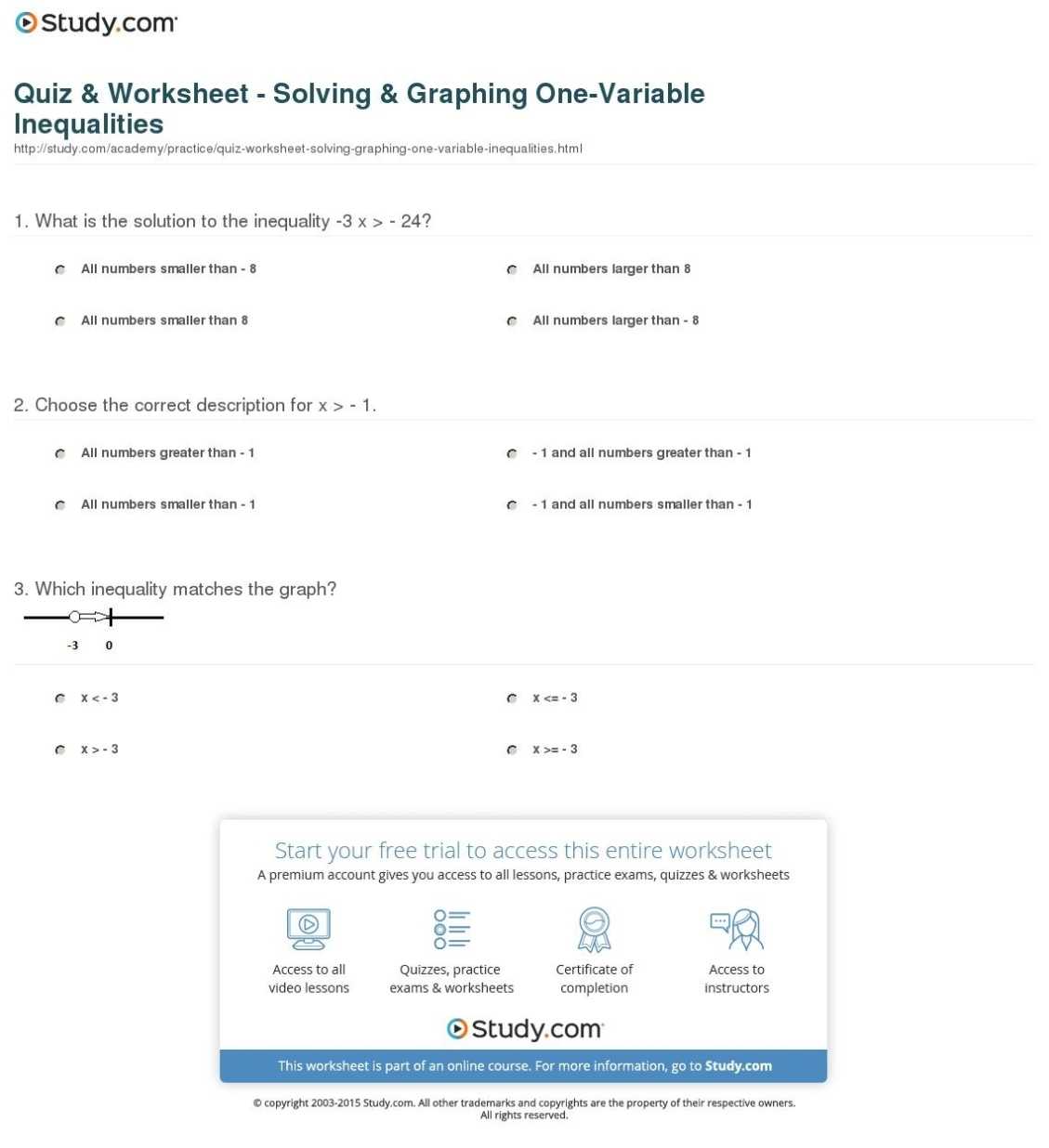
Exploring the Power of Absolute Value Inequalities Worksheet Answers to Help Students Solve Problems

Absolute value inequalities are powerful mathematical tools that can be used to solve a wide range of problems. In order to gain a better understanding of this concept, it is important to first define absolute value. Absolute value is the distance between a given number and zero on a number line. This distance is always positive, regardless of whether the number is positive or negative.

In order to solve an absolute value inequality, students must use the concept of inverse operations. An inverse operation is a mathematical operation that undoes the effect of another operation. For example, adding a number and then subtracting the same number would be an inverse operation.

When solving an absolute value inequality, students must consider the two cases that the inequality could represent. The first case is the case when the absolute value is greater than a given number. In this case, students must choose two numbers that are on opposite sides of the given number and make sure that the absolute value of the difference between them is greater than the given number. The second case is when the absolute value is less than a given number. In this case, students must choose two numbers that are on the same side of the given number and make sure that the absolute value of the difference between them is less than the given number.

In addition to considering the two cases, students should also be aware of the different properties of absolute value inequalities. One of the most important properties is that for any two numbers, the absolute value of their difference is always the same. This property can be used to reduce the amount of calculations that need to be done when solving an absolute value inequality.

By understanding the concept of absolute value and its properties, students can become more confident in their ability to solve absolute value inequalities. With practice and guidance, students can become adept at using this powerful mathematical tool to solve a variety of problems.

Using Absolute Value Inequalities Worksheet Answers to Help Students Grasp Advanced Math Concepts

Absolute value inequalities are a type of advanced mathematical concept that can be difficult for students to grasp. Using a worksheet that includes absolute value inequalities can be a great way to help students understand these concepts and apply them to their own problem solving.

The worksheet should include a variety of equations that require the use of absolute value inequalities. Each equation should be explained clearly and the student should be given ample opportunity to solve the equation. It is important to ensure that the student understands the concept of absolute value and how it applies to the equation before continuing to the next one.

The worksheet should also provide solutions to each equation. This will allow the student to check their work and make sure they have solved each equation correctly. The solutions should also be provided in a step-by-step format so that the student can easily follow along.

Finally, the worksheet should also include a few practice problems. These problems should be designed to help the student apply the concepts they have learned to real-world scenarios. This will ensure that the student is able to effectively use absolute value inequalities in their own problem solving.

By providing a worksheet with absolute value inequalities, students can better understand these advanced mathematical concepts. The worksheet should be well-structured and clear so that the student can understand the equations and solutions easily. It should also provide practice problems to give the student an opportunity to apply the concepts they have learned. With a well-structured worksheet, students can gain a better understanding of absolute value inequalities and use them to their advantage in their own problem solving.

Conclusion

The Absolute Value Inequalities Worksheet Answers provide a great way to understand the concept of absolute value and how it can be applied to inequalities. The questions provided on the worksheet are designed to help students understand the concept in a clear and concise manner, allowing them to apply it to their own situations. By understanding the concept and using it correctly, students can use absolute value inequalities to solve problems in their own lives.

[addtoany]