Exploring the Absolute Value Function: A Step-by-Step Worksheet Guide

Welcome to this step-by-step guide to exploring the absolute value function. This guide will provide you with a comprehensive look at what the absolute value function is, how it works, and how to use it for various purposes.

The absolute value function is a mathematical function that returns the absolute value of any given number. This means that it will always return a positive number, regardless of the sign of the given number. The absolute value of a number is the distance between the number and 0 on the number line.

To understand how the absolute value function works, it is helpful to first look at what absolute values are. Absolute values are always positive numbers, and they are expressed as the distance between a given number and zero. For example, the absolute value of -3 is 3, and the absolute value of 4 is 4.

Next, let’s look at how to use the absolute value function. The absolute value of any given number is expressed as the absolute value symbol, “|x|”. To calculate the absolute value of a number, simply substitute the given number in for x in the absolute value equation. For example, to calculate the absolute value of -3, you would substitute -3 in for x, resulting in |-3| = 3.

Now that we have a basic understanding of how the absolute value function works, let’s look at some examples of how it can be used.

One common use of the absolute value function is to find the distance between two numbers. To do this, simply take the absolute value of the difference between the two numbers. For example, to calculate the distance between 4 and -3, you would take the absolute value of 4 – (-3), which is |4 – (-3)| = 7.

The absolute value function can also be used to calculate the absolute value of an expression. To do this, simply take the absolute value of each term in the expression before combining them. For example, to calculate the absolute value of (3 – 5) + 4, you would take the absolute value of each term, resulting in |3 – 5| + |4| = 2 + 4 = 6.

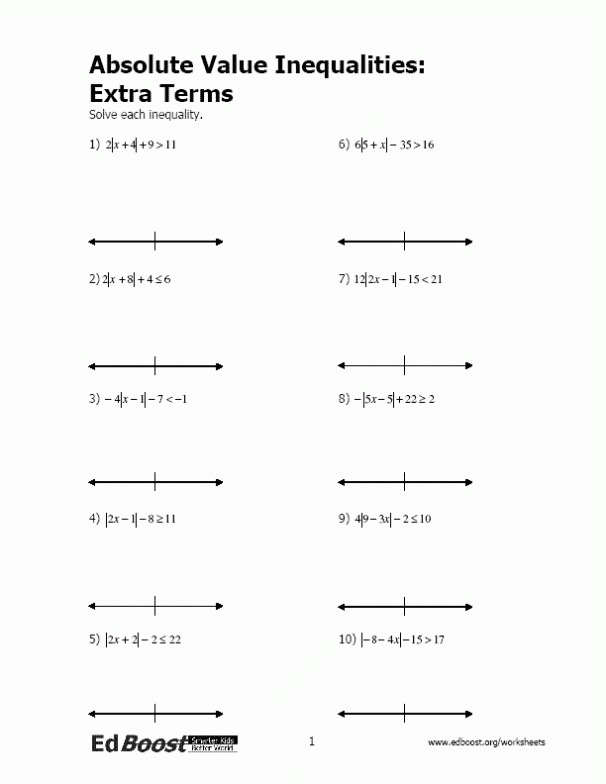
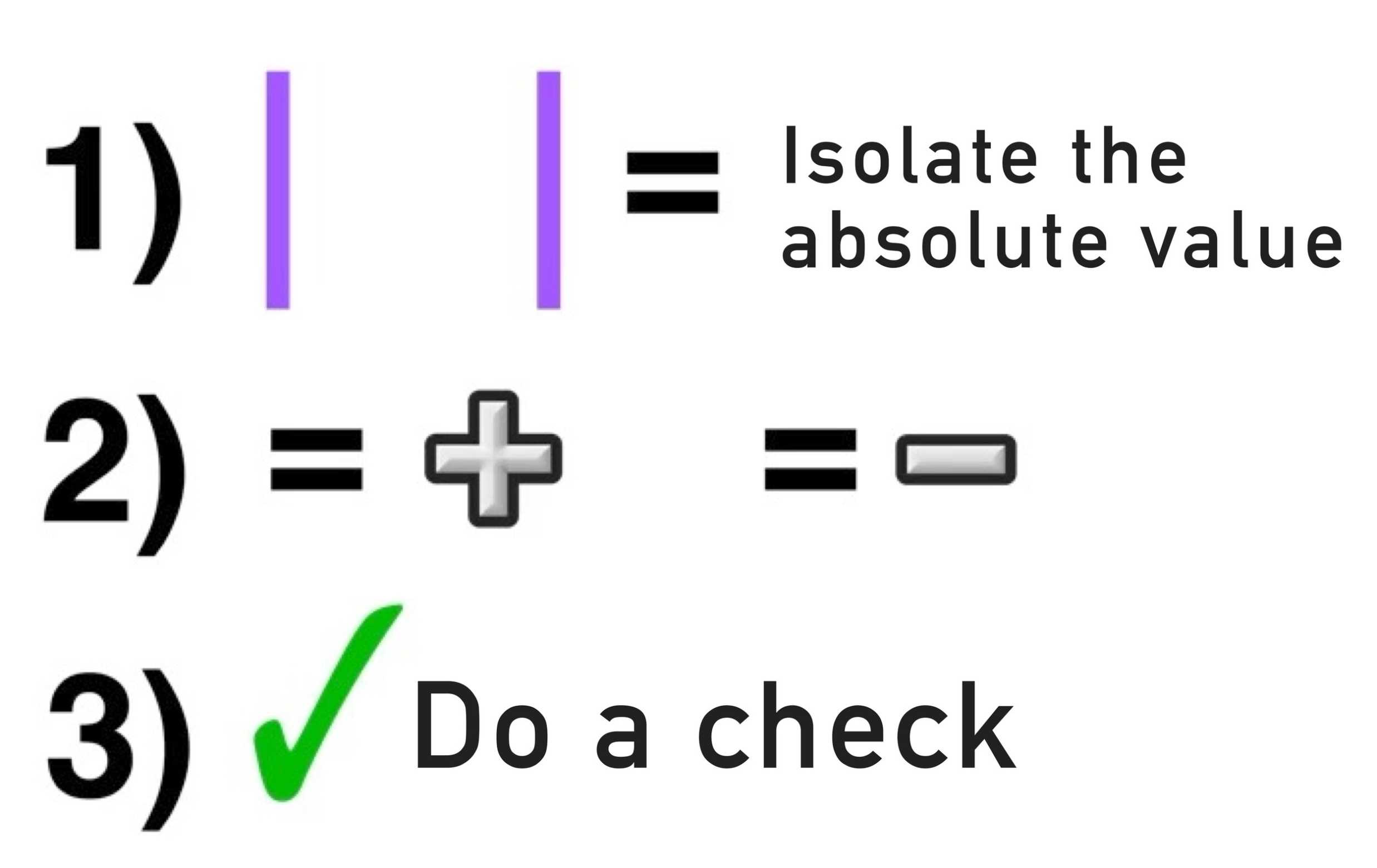
Finally, the absolute value function can also be used to solve equations. To do this, simply isolate the absolute value and solve it as if it were a normal equation. For example, in the equation |x + 3| = 5, you would isolate the absolute value and solve it as if it were a normal equation, resulting in x + 3 = 5 or x = 2.

We hope that this guide has provided you with a comprehensive look at what the absolute value function is, how it works, and how to use it for various purposes. We wish you the best of luck in your mathematical endeavors!

Mastering the Absolute Value Function: Tips & Tricks for Solving Problems on a Worksheet

Applying the Absolute Value Function to Real-World Problems: A Comprehensive Worksheet Guide

The absolute value function is an invaluable tool in mathematics, providing a way to measure distances between two points on a number line regardless of sign. It is a useful tool for solving a wide range of real-world problems, from determining how far away two cities are on a map to measuring the duration of a business trip. This comprehensive worksheet guide is designed to help you understand and apply the absolute value function to real-world problems.

The absolute value of a number is the distance from 0 on the number line, regardless of sign. It is denoted by two vertical lines, such as |-2|, which is equal to 2. This concept can be applied to any number, positive or negative. For example, the absolute value of -5 is 5, and the absolute value of 5 is also 5.

The absolute value function can be used to solve a variety of problems. For example, you can use it to calculate the distance between two points on a number line. To find the distance between two points, subtract the smaller number from the larger one and take the absolute value of the result. For example, if you wanted to find the distance between -3 and 5, you would subtract -3 from 5, which gives you 8. Then, you would take the absolute value of 8, which is 8. Therefore, the distance between -3 and 5 is 8.

The absolute value function can also be used to calculate the difference between two numbers. To find the difference between two numbers, subtract the smaller number from the larger one and take the absolute value of the result. For example, if you wanted to find the difference between 4 and -2, you would subtract -2 from 4, which gives you 6. Then, you would take the absolute value of 6, which is 6. Therefore, the difference between 4 and -2 is 6.

The absolute value function can also be used to measure the duration of a business trip. To find the duration of a business trip, subtract the starting time from the ending time and take the absolute value of the result. For example, if you started your trip at 8 am and ended it at 5 pm, you would subtract 8 from 5, which gives you -7. Then, you would take the absolute value of -7, which is 7. Therefore, the duration of your business trip was 7 hours.

Finally, the absolute value function can be used to measure the distance between two cities on a map. To find the distance between two cities, subtract the x-coordinate of the first city from the x-coordinate of the second city and take the absolute value of the result. Then, subtract the y-coordinate of the first city from the y-coordinate of the second city and take the absolute value of the result. Finally, add the two absolute values together to get the total distance between the two cities.

This comprehensive worksheet guide has provided an overview of the absolute value function and how it can be applied to real-world problems. From calculating the distance between two points on a number line to measuring the distance between two cities on a map, the absolute value function is a powerful tool that can be used to solve a variety of problems.

Analyzing Graphs of Absolute Value Functions: An Interactive Worksheet Guide

Welcome to this interactive worksheet guide on analyzing graphs of absolute value functions. This guide will help you understand the basics of graphing, and then will provide a step-by-step guide on how to interpret and analyze a graph of an absolute value function.

First, let’s define absolute value. Absolute value is a mathematical function that represents the magnitude of a number, regardless of sign. The absolute value of a number x is written as |x| and is equal to the distance between x and zero on a number line. This means that |x| = x if x is positive, and |x| = -x if x is negative.

Now, let’s look at a graph of an absolute value function. An absolute value function is characterized by a V-shaped graph, with the vertex at the origin (0, 0). The graph of the absolute value of x, written as |x|, is a V-shaped graph that is symmetrical about the y-axis. As you move away from the origin in either direction along the x-axis, the graph increases in a linear fashion.

Now that you understand the basics of graphing an absolute value function, let’s look at how to interpret and analyze it. There are several important aspects of the graph that can be used to interpret and analyze it.

First, look at the vertex of the graph. This is the point at which the graph reaches its maximum or minimum value. The x-coordinate of the vertex will tell you whether the absolute value is increasing or decreasing. If the x-coordinate is positive, then the absolute value is increasing. If it is negative, then the absolute value is decreasing.

Next, look at the slope of the graph. This will give you an indication of how quickly the absolute value is changing. If the slope is positive, then the absolute value is increasing. If it is negative, then the absolute value is decreasing.

Finally, look at the asymptotes of the graph. These are the lines that the graph approaches, but never crosses. If the graph is increasing, then the upper asymptote will be the highest value that the absolute value reaches. If the graph is decreasing, then the lower asymptote will be the lowest value that the absolute value reaches.

Now that you know how to interpret and analyze a graph of an absolute value function, you can use this knowledge to answer questions about a given graph. With practice, you will become more familiar with interpreting and analyzing graphs of absolute value functions.

Conclusion

In conclusion, the Absolute Value Function Worksheet is an effective way to understand the concepts behind absolute values and how they can be used to solve equations. It can also be used as a great practice tool for students preparing for exams. The worksheet provides a comprehensive overview of absolute values, their properties, and how to use them to solve equations. With the help of the Absolute Value Function Worksheet, students can gain a better understanding of absolute values and improve their problem-solving skills.