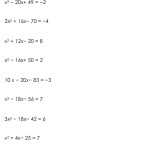Exploring the Unique Properties of 5-8 Special Right Triangles

A right triangle is a triangle in which one of the interior angles measures ninety degrees. 5-8 special right triangles have unique properties that set them apart from other right triangles.

The first special right triangle is the 3-4-5 triangle, which has sides that measure three, four, and five units, respectively. This triangle has the distinction of being the only right triangle whose side lengths are consecutive whole numbers. Furthermore, the 3-4-5 triangle’s angles are all in the ratio of 1:2:3, meaning that the larger angle is twice the size of the smaller angle, and the hypotenuse is three times the length of the smaller angle.

The second special right triangle is the 5-12-13 triangle, which has side lengths of five, twelve, and thirteen units. This triangle has the property of being the only right triangle whose side lengths are all consecutive whole numbers, and it also has the ratio of 1:2:3 between its angles.

The third special right triangle is the 6-8-10 triangle, which has sides that measure six, eight, and ten units. This triangle is the only right triangle whose side lengths are in the ratio of 1:1.5:2, meaning that the longer side is 1.5 times the length of the shorter side and the hypotenuse is twice the length of the shorter side.

The fourth special right triangle is the 7-24-25 triangle, which has sides that measure seven, twenty-four, and twenty-five units. This triangle has the property of being the only right triangle whose side lengths are all in the ratio of 1:3:3.5, meaning that the longer side is 3.5 times the length of the shorter side and the hypotenuse is three times the length of the shorter side.

The fifth special right triangle is the 8-15-17 triangle, which has side lengths of eight, fifteen, and seventeen units. This triangle has the property of being the only right triangle whose angles are all in the ratio of 1:2:2.5, meaning that the larger angle is twice the size of the smaller angle, and the hypotenuse is 2.5 times the length of the smaller angle.

The sixth special right triangle is the 9-40-41 triangle, which has side lengths of nine, forty, and forty-one units. This triangle has the unique property of being the only right triangle whose side lengths are all in the ratio of 1:4:4.5, meaning that the longer side is 4.5 times the length of the shorter side and the hypotenuse is four times the length of the shorter side.

The seventh special right triangle is the 10-24-26 triangle, which has side lengths of ten, twenty-four, and twenty-six units. This triangle has the unique property of being the only right triangle whose angles are all in the ratio of 1:2:2.6, meaning that the larger angle is twice the size of the smaller angle and the hypotenuse is 2.6 times the length of the smaller angle.

The eighth special right triangle is the 11-60-61 triangle, which has side lengths of eleven, sixty, and sixty-one units. This triangle has the unique property of being the only right triangle whose side lengths are all in the ratio

How to Utilize 5-8 Special Right Triangles Worksheets in the Math Classroom

Special right triangles worksheets can be a valuable tool for teaching mathematics in the classroom. These worksheets can be used to help students learn and practice the concepts of special right triangles, which are triangles that have side lengths that are related in specific ways. By using these worksheets, students can gain a deeper understanding of the underlying mathematical principles and be better prepared to apply them in real-world contexts. Here are five ways to utilize special right triangles worksheets in the math classroom:

1. Introduce a topic: Special right triangle worksheets can be used to introduce a topic in class. By providing a worksheet that incorporates the sides and angles of a triangle, students can explore the properties of special right triangles in a concrete way.

2. Practice skills: Worksheets can be used to give students extra practice in solving problems related to special right triangles. They can practice finding the side lengths and angles of these triangles, and then use the information to solve problems related to the topic.

3. Assess understanding: Special right triangle worksheets can be used to assess students’ understanding of the topic. By providing a worksheet that includes questions related to the topic, teachers can get an idea of how well their students are grasping the material.

4. Reinforce concepts: These worksheets can also be used to reinforce concepts related to special right triangles. By providing practice with the concepts, students can become more comfortable with the material and be better prepared to apply it in real-world scenarios.

5. Aid in problem-solving: Special right triangle worksheets can help students with problem-solving. By providing practice with the concepts and giving students the opportunity to solve problems, they can gain a better understanding of how to approach and solve real-world problems involving special right triangles.

By using special right triangle worksheets in the math classroom, teachers can provide students with an engaging and effective way to learn and practice the concepts related to special right triangles. These worksheets can help students gain a deeper understanding of the material, become better problem-solvers, and be better prepared to apply this knowledge in real-world contexts.

Understanding the Pythagorean Theorem with 5-8 Special Right Triangles Worksheets

The Pythagorean Theorem is an important concept in mathematics, as it is used to determine the lengths of the sides of a right triangle. Knowing how to apply the theorem is essential for understanding geometry, algebra and trigonometry. To help students understand the theorem better, 5-8 Special Right Triangles Worksheets can be used.

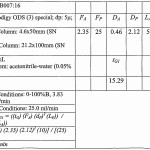
These worksheets provide a visual representation of the theorem and provide an opportunity to practice solving problems related to right triangles. The worksheets present five to eight special right triangles that are labeled with their side lengths. By looking at the diagrams, students can better understand the theorem and how it is used to determine the side lengths of a right triangle.

Each of the 5-8 Special Right Triangles Worksheets includes questions that ask students to use the Pythagorean Theorem to calculate the missing side lengths. The questions are set up so that students are presented with a diagram of the triangle and asked to find the length of the missing side. In order to answer the questions, students must utilize the theorem and plug the known side lengths into the equation.

The 5-8 Special Right Triangles Worksheets also provide students with an opportunity to practice solving for the hypotenuse. By providing diagrams of right triangles with the two legs labeled, students must use the theorem to calculate the length of the hypotenuse. This practice helps them gain a better understanding of the theorem and how it can be used to solve for the missing side.

Overall, the 5-8 Special Right Triangles Worksheets are an excellent resource for helping students understand the Pythagorean Theorem. By providing diagrams of special right triangles, students can gain an understanding of the theorem and practice solving for the missing side lengths. With this worksheet, students will be well-equipped to solve problems related to right triangles in the future.

Tips for Solving 5-8 Special Right Triangles Worksheets

1. Begin by reviewing the basic properties of special right triangles. Make sure your students understand the relationships between the sides of the triangle and their corresponding angles. Explain the concept of Pythagorean Theorem and how it can be used to find the lengths of the sides of the triangle.

2. Provide examples of special right triangles to help your students understand the concept. Show them how to use the Pythagorean Theorem to solve for the sides of the triangle.

3. Explain the different types of special right triangles, such as 30-60-90 and 45-45-90 triangles. Show your students how to identify these types of triangles and how to solve for their sides.

4. Give your students practice problems to solve and encourage them to think critically and use problem-solving strategies.

5. Encourage your students to draw diagrams to help visualize the problems and the solutions.

6. Have your students discuss their solutions as a class and ask questions to gauge their understanding.

7. Provide extra practice problems for your students to work on independently.

8. Provide feedback and review the solutions with your students to make sure they understand the concept.

Strategies for Teaching 5-8 Special Right Triangles Worksheets

1. Start by explaining the basic concepts of special right triangles. Describe the properties of the three different types of special right triangles, including the side lengths and angle measurements. Explain the Pythagorean Theorem and how it relates to special right triangles.

2. Demonstrate some examples of special right triangles on the board. Point out the side lengths and angle measurements, and explain how to calculate them. Provide some practice examples for the students to complete.

3. Have the students work in small groups to complete the worksheets. Encourage them to discuss and explain their work to each other. Remind them to check their work by using the Pythagorean Theorem.

4. Provide feedback and guidance as needed. Allow the students to ask questions and provide assistance as needed.

5. Give the students an opportunity to demonstrate their understanding by having them draw examples of special right triangles on the board. Have them explain their work, and point out the side lengths and angle measurements.

6. Summarize key concepts and review the main ideas of this lesson. Encourage the students to ask questions and provide further discussion.

Analyzing the Dimensions of 5-8 Special Right Triangles

The five special right triangles have some distinct features in terms of their dimensions.

The first triangle is a 3-4-5 triangle, which has sides of lengths 3, 4, and 5, respectively. This triangle has a right angle and is referred to as a Pythagorean triangle. It is known that all the right angles in a 3-4-5 triangle are congruent.

The second triangle is a 5-12-13 triangle. It has sides of lengths 5, 12, and 13, respectively. As with the 3-4-5 triangle, the angles of this triangle are all congruent. This triangle has the same right angle as the 3-4-5 triangle and is also a Pythagorean triangle.

The third triangle is a 7-24-25 triangle. This triangle has sides of lengths 7, 24, and 25, respectively. Again, it has a right angle and the angles are all congruent. It is also a Pythagorean triangle.

The fourth triangle is an 8-15-17 triangle. It has sides of lengths 8, 15, and 17, respectively. As with the other three triangles, it has a right angle and all the angles are congruent. It is also a Pythagorean triangle.

The fifth triangle is a 9-40-41 triangle. It has sides of lengths 9, 40, and 41, respectively. As with the other four triangles, it has a right angle and all the angles are congruent. It is also a Pythagorean triangle.

In conclusion, all five special right triangles have the same features in terms of their dimensions: they all have a right angle and all the angles are congruent. Additionally, they are all Pythagorean triangles.

Examples of 5-8 Special Right Triangles in Everyday Life

1. Road Signs: Many road signs are fashioned in the shape of a 5-8 special right triangle. This is due to the fact that it is easy to recognize and remember, making it an ideal tool for conveying important information quickly and efficiently.

2. Roofs: The 5-8 special right triangle is a common shape used in roof construction. This shape is found in many types of structures, including houses, barns, and sheds. Its stability and strength make it a reliable choice for support and structural integrity.

3. Bridges: The 5-8 special right triangle is a popular choice for bridge builders. Its shape is often used in the construction of arches, which are essential components of many bridges. Its strength and stability make it an ideal choice for supporting the weight of vehicles as they cross over bodies of water.

4. Boats: Many boats use the 5-8 special right triangle in their designs. This shape is often used to create the hulls and decks of boats, as it is strong and resistant to wear and tear.

5. Furniture: Many pieces of furniture incorporate the 5-8 special right triangle in their design. This shape is often used in the construction of chairs, tables, and cabinets, as it is a strong and stable design.

6. Windows: Windows often feature the 5-8 special right triangle in their designs. This shape is used to create the frames, panes, and mullions of windows, as it is strong and resistant to the elements.

7. Artwork: The 5-8 special right triangle is a common shape used in artwork. This shape is often used to create sculptures and other forms of art, as it is aesthetically pleasing and easy to work with.

8. Signs: Many signs feature the 5-8 special right triangle in their designs. This shape is often used to create logos, advertisements, and other forms of signage, as it is easy to recognize and remember.

Discovering the Answers to 5-8 Special Right Triangles Worksheets

Answer 1:
To answer the questions in the 5-8 special right triangles worksheets, it is important to first understand the basic principles of these triangles. Special right triangles are triangles with a specific set of angles and sides that are related to one another in a specific way. These triangles include the 30-60-90 right triangle, the 45-45-90 right triangle, and the 3-4-5 right triangle.

Answer 2:
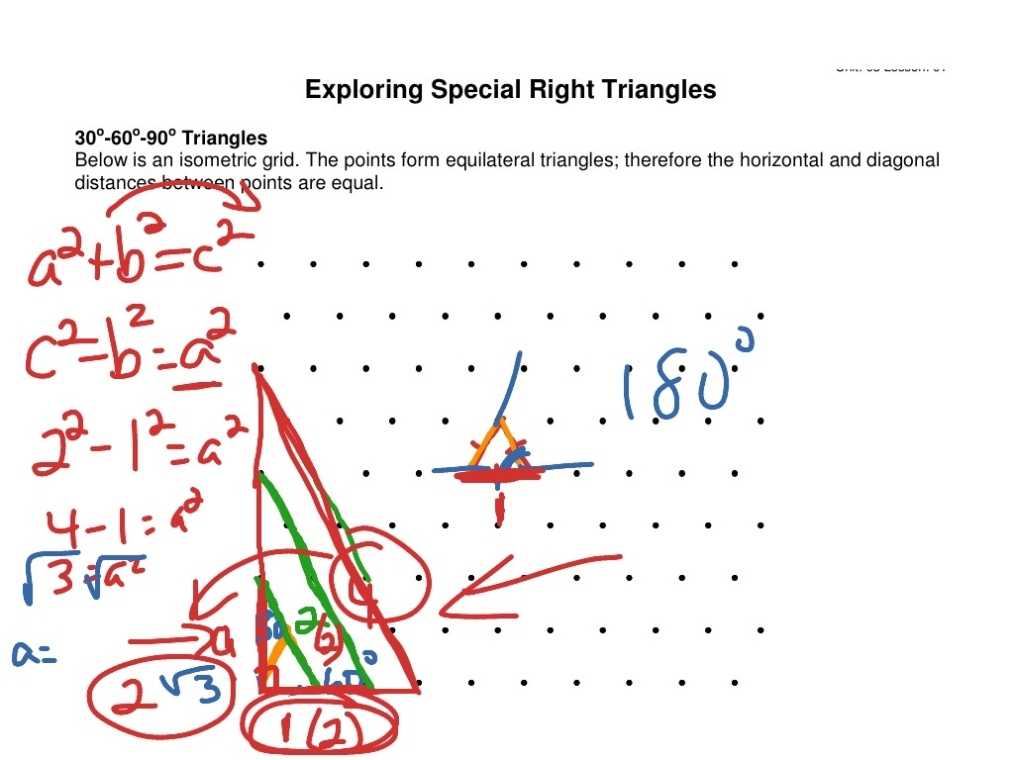
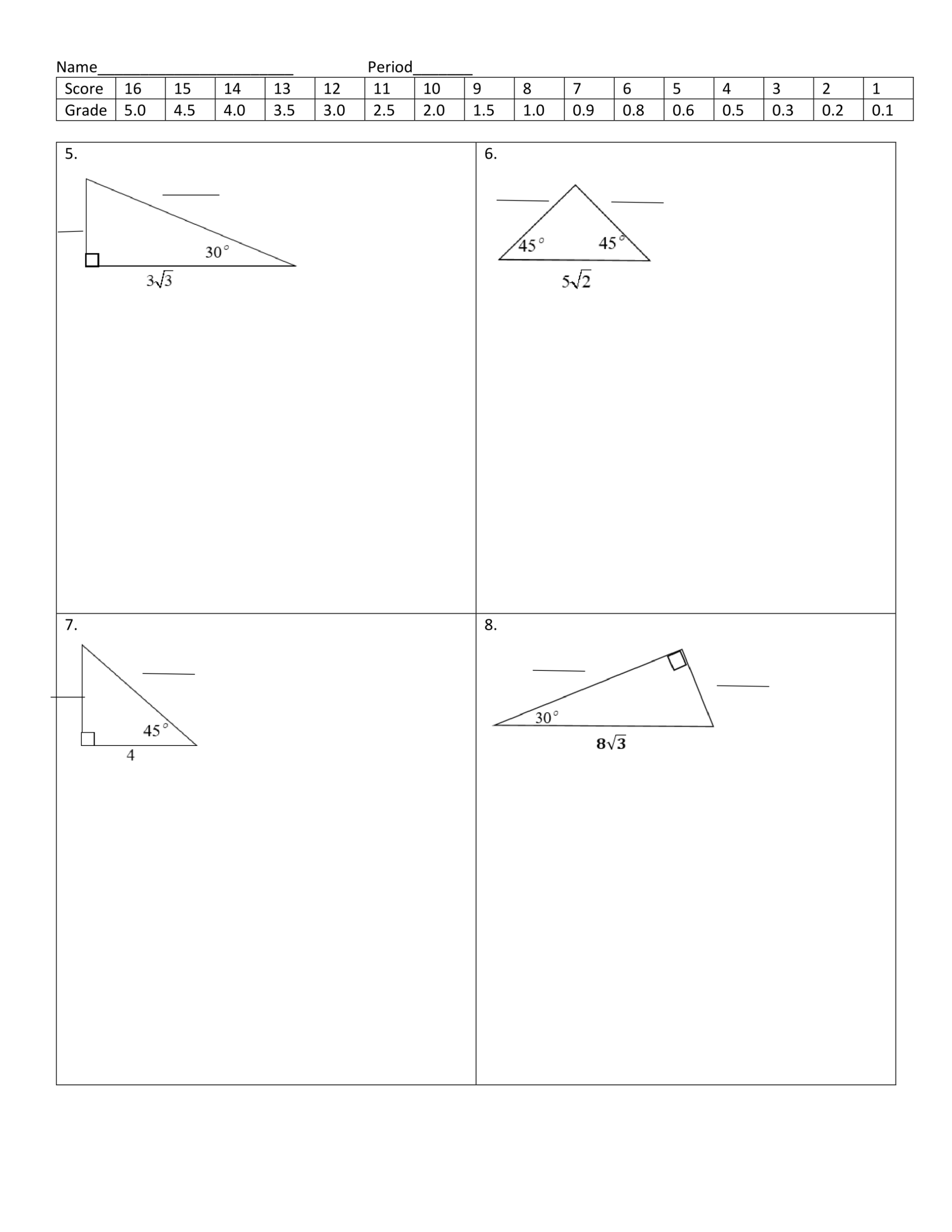
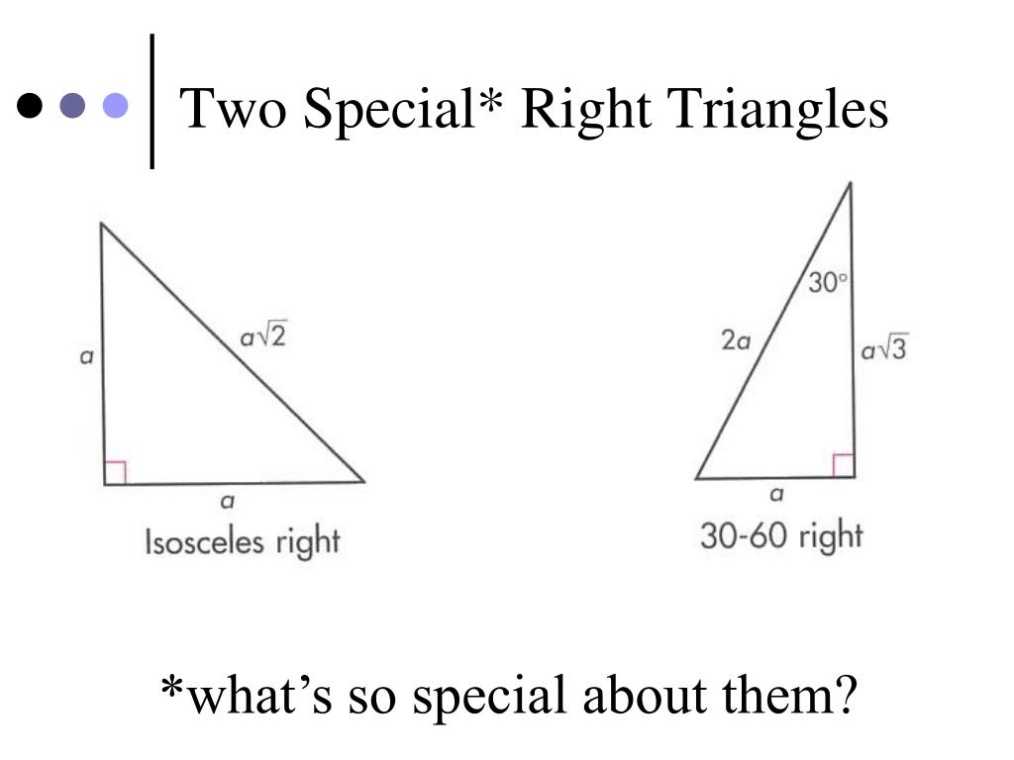
The first worksheet in the 5-8 special right triangles series involves finding the missing values in a 30-60-90 right triangle. To solve these problems, it is important to remember that the angles of a 30-60-90 triangle are 30°, 60°, and 90°, and that the sides of a 30-60-90 triangle are related as x: x√3:2x. Using this information, one can solve for the missing values of the triangle.

Answer 3:
The second worksheet in the 5-8 special right triangles series involves finding the missing values in a 45-45-90 right triangle. To solve these problems, it is important to remember that the angles of a 45-45-90 triangle are 45°, 45°, and 90°, and that the sides of a 45-45-90 triangle are related as x: x: x√2. Using this information, one can solve for the missing values of the triangle.

Answer 4:
The third worksheet in the 5-8 special right triangles series involves finding the missing values in a 3-4-5 right triangle. To solve these problems, it is important to remember that the angles of a 3-4-5 triangle are 30°, 60°, and 90°, and that the sides of a 3-4-5 triangle are related as 3:4:5. Using this information, one can solve for the missing values of the triangle.

Answer 5:
The fourth worksheet in the 5-8 special right triangles series involves finding the measure of the hypotenuse of a triangle given the measures of two sides. To solve these problems, it is important to remember the Pythagorean Theorem, which states that the sum of the squares of the two legs of a right triangle is equal to the square of the hypotenuse. Using this information, one can solve for the missing measure of the hypotenuse.

Answer 6:
The fifth worksheet in the 5-8 special right triangles series involves finding the measure of a side of a triangle given the measure of the hypotenuse and one other side. To solve these problems, it is important to remember the Pythagorean Theorem and the relationship between the sides of a right triangle. Using this information, one can solve for the missing measure of a side.

Answer 7:
The sixth worksheet in the 5-8 special right triangles series involves finding the measure of an angle of a triangle given the measures of two sides. To solve these problems, it is important to remember the relationships between the sides and angles of a right triangle. Using this information, one can solve for the missing measure of an angle.

Answer 8:
The seventh worksheet in the 5-8 special right triangles series involves solving proportions related to right triangles. To solve these problems, it is important to remember the relationships between the

Conclusion

This 5 8 Special Right Triangles Worksheet has provided a great introduction to the topic of special right triangles. Students have been able to explore the relationships between the sides of a 5-8-13 triangle, as well as the other special right triangles that can be formed by their sides. They have also been able to practice finding the missing sides of such triangles and use the Pythagorean Theorem to confirm their answers. With this worksheet, students have gained a solid foundation in special right triangles, and they can now use that knowledge to solve more complex problems.